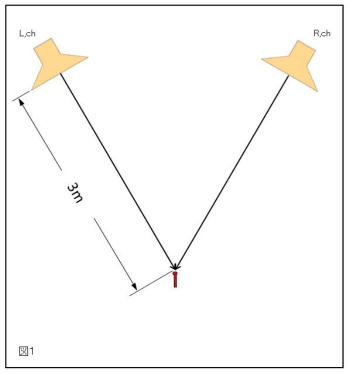
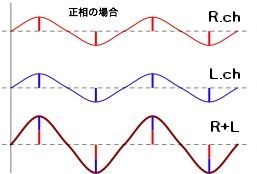
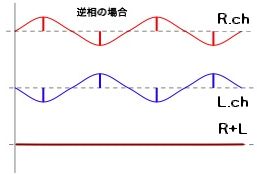
⑨音が消える
    |
例えばこんな実験をしてみたとします。 左右のスピーカーどちらからも３ｍの位置にマイクを立て、周波数１，０００Hzの音を出しマイクで拾ってみます。 本来は 音速[m/s] = 331.5＋0.6t t：温度（摂氏℃）で計算できますが、ここでは解りやすいように音速 300ｍとして計算します。 波長λ[m] = 音速V[m/s] ／周波数 f[Hz]の関係式より周波数１，０００Hｚの音の波長は0.3ｍ（30ｃｍ）となります。 従って、スピーカーから出た１，０００Hzの音は、３ｍ先のマイクに到着するまで、１０波長要するという事になります。 どちらのスピーカーからも等距離ですので、マイクに到達する時は同じ形の波になり、位相のずれはありません。 この様な状態を正相と呼びます。 この場合、左右のスピーカーから出てマイクに到着した音の強さは、単純に足し算すれば求められるという事になります。 左の図の山谷の膨らみを振幅と言いますが、これが音の強さを表します。 左右チャンネルの音が正相の場合、合成された波は振幅が２倍になった波として表され、これは音の強さが２倍になったことを意味します。 普通、ステレオ装置で音楽を聴く場合、このように左右の音の足し算された物を聴いている訳です。 今度は、右スピーカーからの距離は同じ３ｍでも、左スピーカーからは３ｍ１５ｃｍ離れた場所にマイクを立て、先ほどと同じ１，０００Hzの音を出し測定してみましょう。 右スピーカーから出た１，０００Hzの音は、マイクに到着するまで１０波長要するのは同じですが、左のスピーカーから出た音は、距離が１５ｃｍ伸びている為、あと半波長必要となります。 この時の波形は、山と谷がちょうど逆になった形となり、位相が１８０度ずれる事になります。この様な状態を逆相と呼びます。 同じ強さの逆相の波を合成した場合、山と谷が重なり合う事になり、それらが打ち消し合い結果的に振幅ゼロという事になります。 という事でこの場合、何も聞こえないという事になります。 （実際には、この場合は等距離ではありませんので、音の強さに差が生じることにより、完全に無音になる事はないでしょう。） |
以上の事はあらゆる周波数で起きます。完全に逆相にはならない場合でも位相のずれはほぼ必ず起き、センターからずれた位置では、左右の波の干渉により音源と同じ波形の音を聴いている事にはなりません。
「⑤定位の良さとは」 で左右の周波数特性は同一にしなければいけないという事を書きましたが、以上のことから、聴く位置も左右スピーカーから等距離の場所をきっちり確保しなければいけません。
スピーカーの調整を行う場合、まずリスニングポイントの正確な位置決めを行い、その上で実行する必要があります。
という訳で、座った位置がいつも同じになるように、部屋は対象に使い、スピーカーを対象に置き、対面の壁にセンターを示す目印を付けておくことが必要かと思います。
そのセンターに音がきっちり留まるよう左右の周波数特性を調整していく訳です
２０24年1月3日 追記 正確なセンターの位置取りの仕方思いつきました。 詳しくは こちら をお読み下さい。
音源が複数ある場合、必ず音の干渉が起きる訳で、部屋で音楽を聴く場合、左右のスピーカーから出る音が干渉し合っているという事ですが、さて、部屋の中でスピーカー以外に音源に成り得る物は他にはないのでしょうか？
スピーカーから出た音は放射状に広がって行き、部屋の壁、床、天井に何度も反射しながら減衰し消えて行きます。
仮に残響時間が０．５秒の六畳間で考えてみますと、いったん出た音は５０回程も反射を繰り返すという事になります。 それらの反射音は一旦コーナーに集まり、そこからまた空間に向かって放射されて行きます。このコーナーに集められた音はエネルギーが凝縮された状態で、その放射方向はそのコーナーの空間の中心から放射状に、すなわちリスニングポイントの近くに向かって行くのでしょう。
音のエネルギーの強さは距離の２乗に反比例しますから、反射を繰り返した音のエネルギーはスピーカーから直接出た音のエネルギーに比べるととても小さいはずなんですが、このコーナーから放出される音は再生音に重大な影響を及ぼしているようです。
あたかも、それがスピーカー以外の音源になったかの如く。つまりは、部屋に都合１０個（２個のスピーカーと８個のコーナー）の音源が存在しているかのようです。
それら１０個の音源から出る音の合成音を私たちは聴いている訳で、つまりCDに録音されている音は、今聴いている音とは全く別の物であるという事が出来ます。
部屋に存在する八つのコーナーのうち、特に大きな影響を及ぼすのは、スピーカー後方の左右の、床と天井の四つのコーナーだと思われます。
このコーナーからの放射音がスピーカーから出る音にどんな風に影響を及ぼすのか考えてみます。
 |
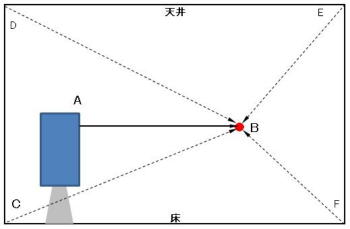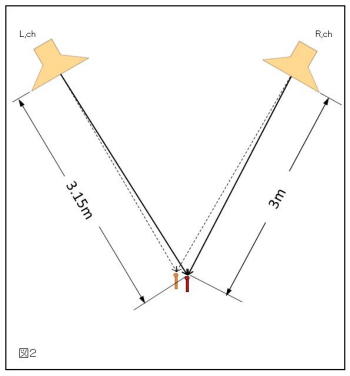
左の図でAがスピーカー、Bが耳の位置、コーナーは４ヶ所ありますが、スピーカー裏のコーナーCについて話をします。 一般的にツイーターの位置を耳の位置に合わせるようにセッティングしますので、このような書き方をしていますが、A―Bはスピーカー各ユニットからの平均距離とお考え下さい。 |
ある周波数ｆ（Ｈｚ）の音をスピーカーＡから出した時、Ｂに到達するのに要する波長数をｘとし、コーナーＣからの反射音がＢに到達するのに要する波長数をｙとしますと
このx、yを求める式は
ｘ＝Ｘ（A－B間の距離）÷λ（波長） ここで λ（波長）＝Ｖ（音速）÷ｆ（周波数） ですので、
ｘ＝Ｘ÷Ｖ÷ｆで求められます。
同様に
ｙ＝Ｙ÷Ｖ÷ｆで求められます。
今、Ｘ（A－B間の距離）＝３ｍ Ｙ（Ｃ－Ｂ間の距離）＝４．３５ｍとした時のＢまでの波長数x, yと位相差を計算すると下の表の様になります。（ここでも便宜上、音速Ｖ＝３００ｍとして計算しています。）
| 周波数(Hz) | 波長(m) | x | y | 位相差(度) | 備考 |
|---|---|---|---|---|---|
| 100 | 3.000 | 1.0 | 1.45 | 162 | |
| 200 | 1.500 | 2.0 | 2.90 | 324 | |
| 300 | 1.000 | 3.0 | 4.35 | 126 | |
| 400 | 0.750 | 4.0 | 5.80 | 288 | |
| 500 | 0.600 | 5.0 | 7.25 | 90 | |
| 600 | 0.500 | 6.0 | 8.70 | 252 | |
| 700 | 0.429 | 7.0 | 10.15 | 54 | |
| 800 | 0.375 | 8.0 | 11.60 | 216 | |
| 900 | 0.333 | 9.0 | 13.05 | 18 | |
| 1,000 | 0.300 | 10.0 | 14.50 | 180 | 逆相（ディップ） |
| 1,100 | 0.273 | 11.0 | 15.95 | 342 | |
| 1,200 | 0.250 | 12.0 | 17.40 | 144 | |
| 1,300 | 0.231 | 13.0 | 18.85 | 306 | |
| 1,400 | 0.214 | 14.0 | 20.30 | 108 | |
| 1,500 | 0.200 | 15.0 | 21.75 | 270 | |
| 1,600 | 0.188 | 16.0 | 23.20 | 72 | |
| 1,700 | 0.176 | 17.0 | 24.65 | 234 | |
| 1,800 | 0.167 | 18.0 | 26.10 | 36 | |
| 1,900 | 0.158 | 19.0 | 27.55 | 198 | |
| 2,000 | 0.150 | 20.0 | 29.00 | 0 | 正相（ピーク） |
| 2,100 | 0.143 | 21.0 | 30.45 | 162 | |
| 2,200 | 0.136 | 22.0 | 31.90 | 324 | |
| 2,300 | 0.130 | 23.0 | 33.35 | 126 | |
| 2,400 | 0.125 | 24.0 | 34.80 | 288 | |
| 2,500 | 0.120 | 25.0 | 36.25 | 90 | |
| 2,600 | 0.115 | 26.0 | 37.70 | 252 | |
| 2,700 | 0.111 | 27.0 | 39.15 | 54 | |
| 2,800 | 0.107 | 28.0 | 40.60 | 216 | |
| 2,900 | 0.103 | 29.0 | 42.05 | 18 | |
| 3,000 | 0.100 | 30.0 | 43.50 | 180 | 逆相（ディップ） |
| 3,100 | 0.097 | 31.0 | 44.95 | 342 | |
| 3,200 | 0.094 | 32.0 | 46.40 | 144 | |
| 3,300 | 0.091 | 33.0 | 47.85 | 306 | |
| 3,400 | 0.088 | 34.0 | 49.30 | 108 | |
| 3,500 | 0.086 | 35.0 | 50.75 | 270 | |
| 3,600 | 0.083 | 36.0 | 52.20 | 72 | |
| 3,700 | 0.081 | 37.0 | 53.65 | 234 | |
| 3,800 | 0.079 | 38.0 | 55.10 | 36 | |
| 3,900 | 0.077 | 39.0 | 56.55 | 198 | |
| 4,000 | 0.075 | 40.0 | 58.00 | 0 | 正相（ピーク） |
| 4,500 | 0.067 | 45.0 | 65.25 | 90 | |
| 5,000 | 0.060 | 50.0 | 72.50 | 180 | 逆相（ディップ） |
| 5,500 | 0.055 | 55.0 | 79.75 | 270 | |
| 6,000 | 0.050 | 60.0 | 87.00 | 0 | 正相（ピーク） |
| 6,500 | 0.046 | 65.0 | 94.25 | 90 | |
| 7,000 | 0.043 | 70.0 | 101.50 | 180 | 逆相（ディップ） |
| 7,500 | 0.040 | 75.0 | 108.75 | 270 | |
| 8,000 | 0.038 | 80.0 | 116.00 | 0 | 正相（ピーク） |
| 8,500 | 0.035 | 85.0 | 123.25 | 90 | |
| 9,000 | 0.033 | 90.0 | 130.50 | 180 | 逆相（ディップ） |
| 9,500 | 0.032 | 95.0 | 137.75 | 270 | |
| 10,000 | 0.030 | 100.0 | 145.00 | 0 | 正相（ピーク） |
| 10,500 | 0.029 | 105.0 | 152.25 | 90 | |
| 11,000 | 0.027 | 110.0 | 159.50 | 180 | 逆相（ディップ） |
| 11,500 | 0.026 | 115.0 | 166.75 | 270 | |
| 12,000 | 0.025 | 120.0 | 174.00 | 0 | 正相（ピーク） |
| 12,500 | 0.024 | 125.0 | 181.25 | 90 | |
| 13,000 | 0.023 | 130.0 | 188.50 | 180 | 逆相（ディップ） |
| 13,500 | 0.022 | 135.0 | 195.75 | 270 | |
| 14,000 | 0.021 | 140.0 | 203.00 | 0 | 正相（ピーク） |
| 14,500 | 0.021 | 145.0 | 210.25 | 90 | |
| 15,000 | 0.020 | 150.0 | 217.50 | 180 | 逆相（ディップ） |
| 15,500 | 0.019 | 155.0 | 224.75 | 270 | |
| 16,000 | 0.019 | 160.0 | 232.00 | 0 | 正相（ピーク） |
この表からも解る通り、スピーカーから出る音はコーナーからの反射音の干渉を受け、常に歪んだ状態の波形を描くことになり、特に１，０００Ｈｚ毎にディップとピークが交互に現れる事になります。
周波数特性グラフのＸ（横）軸は対数表示されている事でお解りのように、高音になる程その間隔は詰まって聞こえてきますので、３，０００Ｈｚ以上において、１，０００Ｈｚごとに山谷が現れる事は音質に相当な影響を与えることが想像できます。
この項「⑩音場の出現」に続く
